1. Abstract
Johann Wolfgang Goethe has been working on his drama Faust for almost his entire life. As witnesses of his work, 556 manuscripts are currently known. Together with the 15 relevant prints that have been published during Goethe’s lifetime, a newly constituted text and supplementary material have been published in a hybrid edition (Goethe 2019).
The edition aims to provide insight into the genesis of the drama’s text. Yet, the order in which the individual manuscripts have been created as well as the dating of the acts of inscription are subject to more than 100 years of research and editorial activity. Most studies only deal with a handful of witnesses and provide either a relative chronology or a broad dating for them. The only attempts to aggregate individual statements in order to place all relevant objects in a chronological-stemmatic relation to date have been provided by Renate Fischer-Lamberg. Her stemmata for two acts of Faust II (Fischer-Lamberg 1955, 150–66) probably mark the practical limit of how much of this information can be gasped by human means alone.
Basic graph model
In order to facilitate algorithmic aggregation, the edition project has first formalized the assertions from the research literature as illustrated in fig. 1.
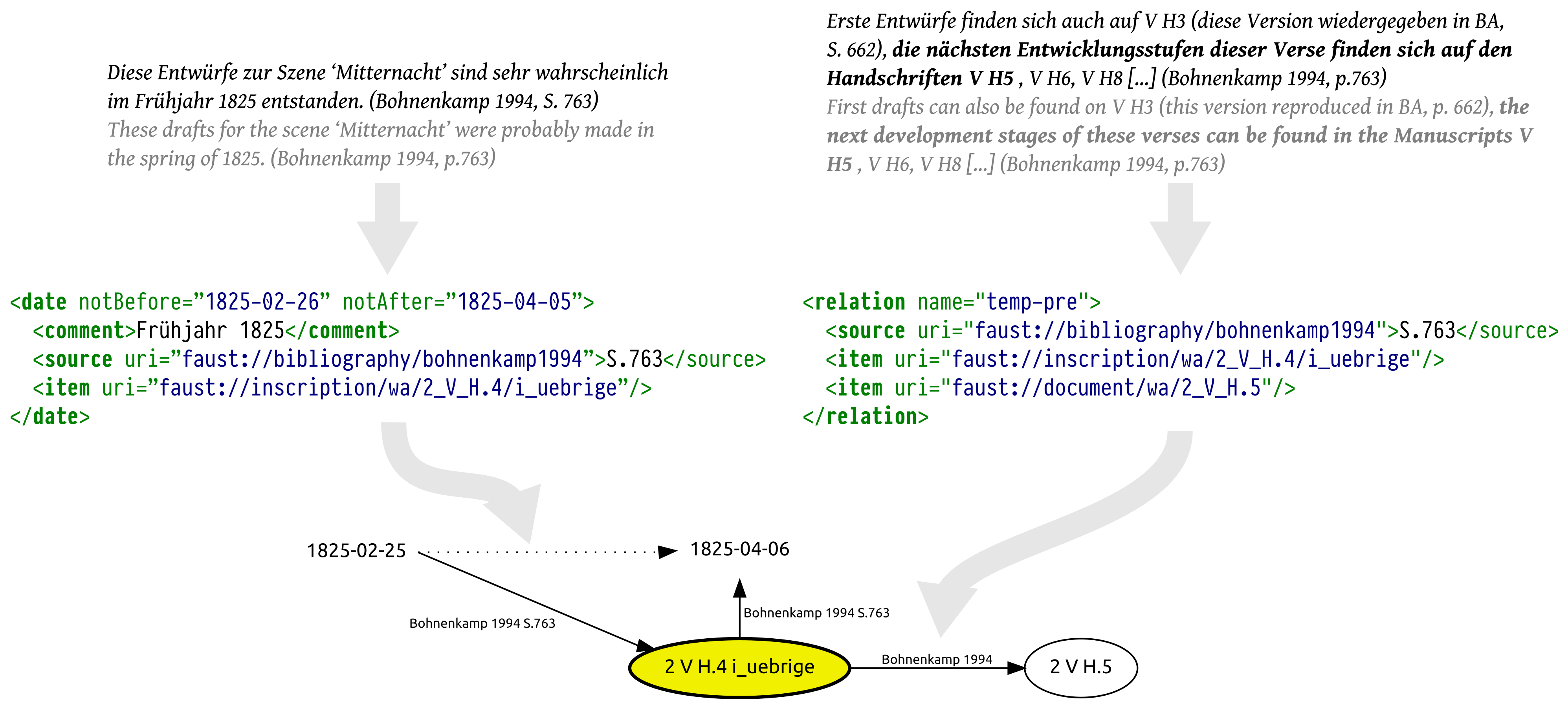
Figure 1: Formalizing absolute datings and relative chronologies from literature, and including them in a common graph model (Vitt and Brüning 2019)
Early attempts of working with the data used logic solvers and a set of rules to infer new, derived assertions (Wissenbach, Pravida, and Middell 2012). In the current approach, graph based models are used since they provide dual benefit: There is a wealth of algorithms to answer various questions on graphs, and subgraphs can be easily visualized in order to understand and justify a certain witness’s dating.
The basic model combines all formalized assertions into a single directed multi-graph as illustrated in fig. 1. Under the assumptions that all assertions are correct, we can now infer an order that is consistent with all assertions (a topological sorting (Kahn 1962)), and we might be able to infer or improve limits for the absolute dating of a witness by looking for the nearest reachable dates in the graph.
Conflicts
Unfortunately, there are contradictions between some of the assertions. In the graph, contradictions appear as cycles and prevent both kinds of deduction outlined above. Since the data features a strongly connected component with 477 documents and 2136 edges inducing millions of cycles, it is not possible to determine manually which edges best to remove to make the graph acyclic. While this problem generally is NP-hard (Karp 1972), an algorithm by Baharev, Schichl, and Neumaier (2015) solves it for our graph, suggesting a relatively small subset of edges to remove (171 of 3480). Edge weights based on the assertions’ sources influence this algorithm.
For each automatically determined conflict, a visualisation indicating conflicting assertions makes it easy to manually check against the original sources (fig. 2). The result can be fed back into the data by assigning edges a specificly large or low weight.

Figure 2: Conflict visualization for an automatically discarded edge (dashed red)
Inscriptions
To complicate things further, a single document may contain multiple inscriptions (Hoenen and Brüning 2019), i.e., it may have been written on in completely separate working phases. E.g., the single sheet 2 II H.5 (cf. fig. 2) has verses belonging to different parts of Faust on the recto and verso side, so Bohnenkamp (1994) deduced from what is known about Goethe’s working phases that they might have been written 25 years apart. (Brüning and Hahn (2017) show both sides are written with the same ink, indicating synchronicity instead).
There are assertions both on inscriptions as well as on their respective witness as a whole (fig. 3), and it is not always clear or consistent between authors which parts of the text belong to which inscription.
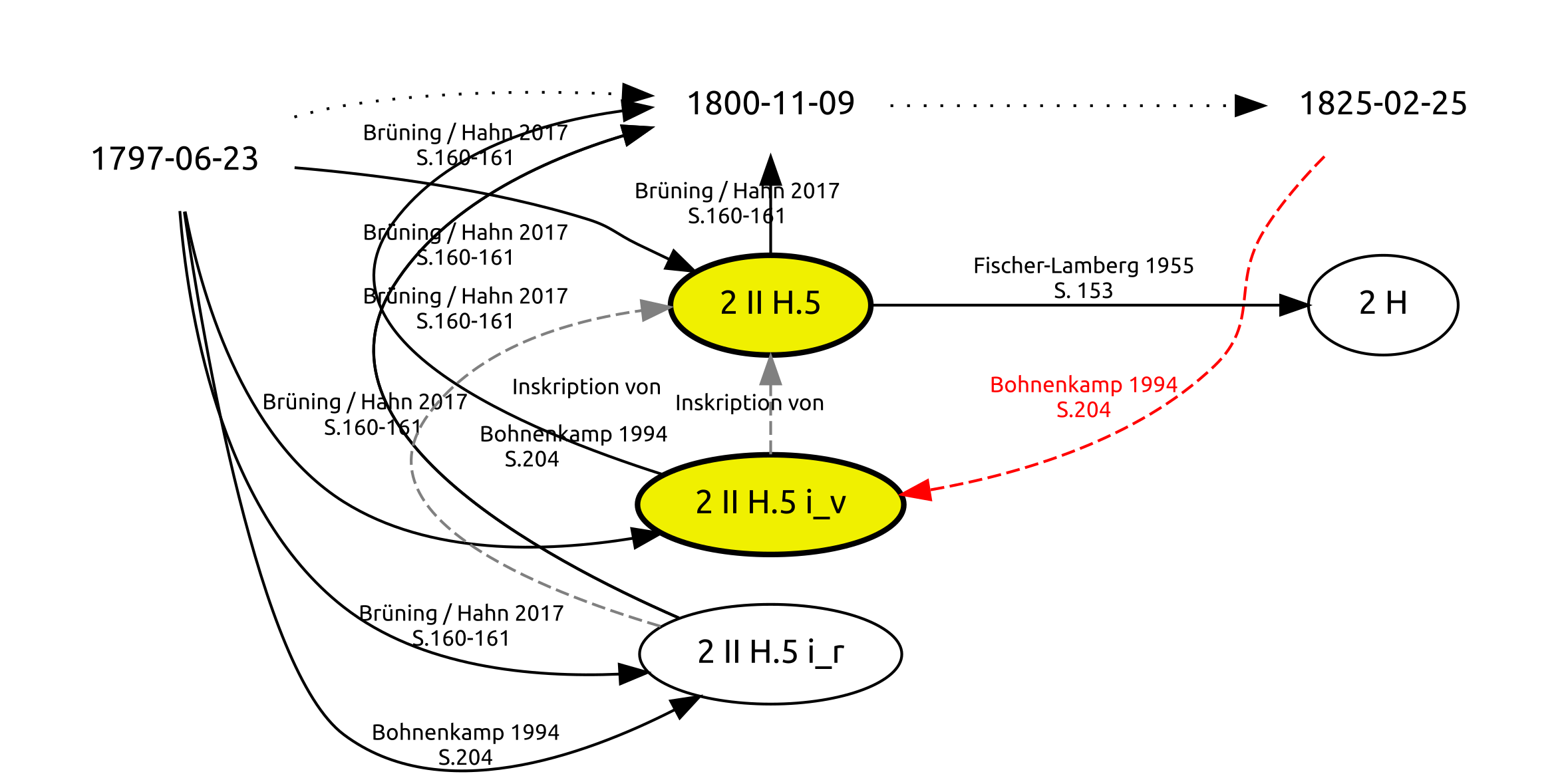
Figure 3: 2 II H.5 and its inscriptions
Model variants
There have been experiments with variants on the model to deal with these differences:
Copying information about inscriptions to their corresponding witnesses changed the ordering of 17 datable objects.
Research literature provides a few assertions about “approximately synchronous” witnesses. To include this information, incoming and outgoing edges have been distributed within each group of synchronous witnesses. This induced absolute datings for more nodes, and it also changed the ordering for up to 67 objects.
Witnesses and inscriptions were modelled using two linked nodes each, representing the start and end of the working phase. All incoming edges end at the start node, all outgoing edges emerge from the end node, and inscriptions are linked to their inscription in order to happen ‘during’ the timespan of the witness (fig. 4). This model decreased the conflicting edges (to 139), and it has some influence on the ordering.
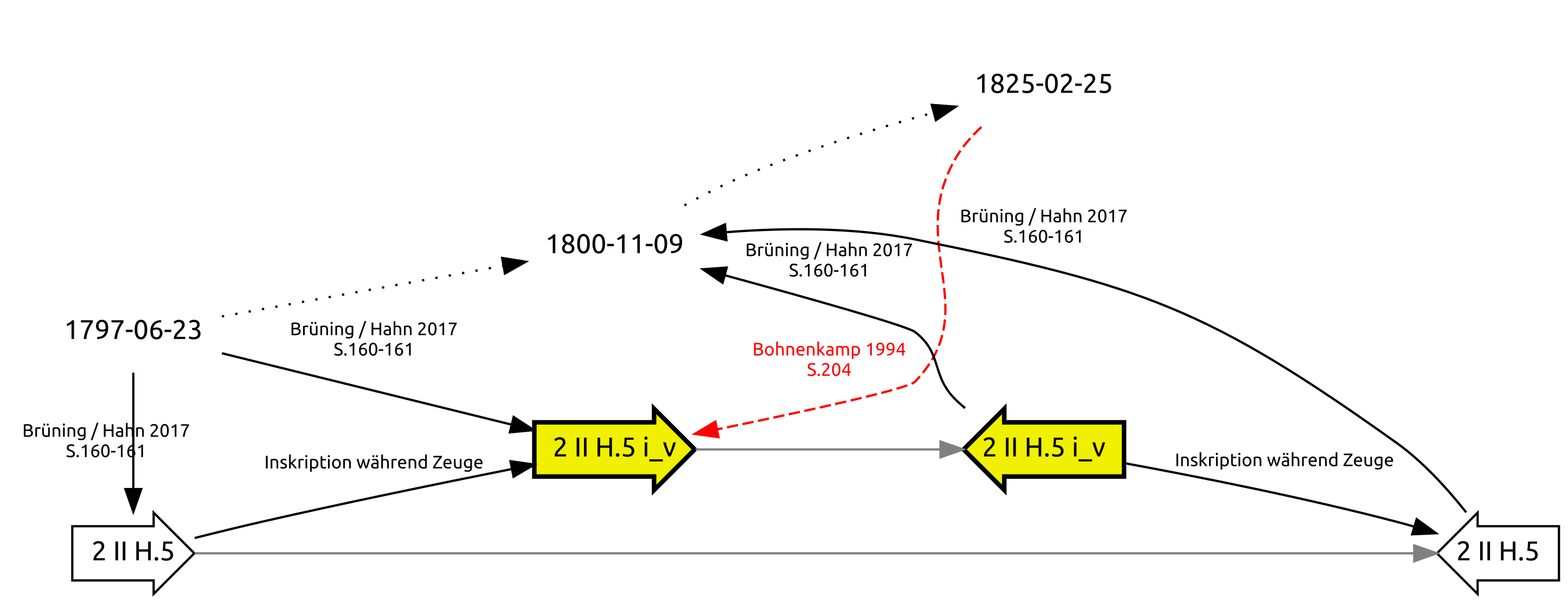
Figure 4: Working phase as interval
Evaluation
There is no pre-known correct ordering to use as a gold standard for evaluation. However, a few measurable values indicate a better model:
- Less conflicting edges reduce the workload for manual review.
- The number of nodes for which a not-before or not-after limit could be inferred hints at the usefulness of the model.
- Different orderings of the witnesses can be compared, e.g. by using a rank correlation like Spearman’s Rank Correlation based on the mean squared difference between the respective ranks of all nodes in two rankings.
Further work
Fig. 4 models witnesses as intervals. This could be improved by modelling everything as intervals and allowing all 13 possible relations in between. Allen (1983) developed a graph model for this, but that does not provide conflict resolution out of the box.
Vague absolute datings line “spring 1825” are normalized to standard crisp intervals. Research, e.g., by Holmen and Ore (2010) uses fuzzy sets to model fuzzy intervals, and Schockaert and De Cock (2008) define relations and inference on such fuzzy intervals. Whether this approach is tractable for our data still needs to be determined.
Open data
All source data and generated graphs as well as the software library developed to analyse and visualize them are publicly and freely available (sources and software at https://github.com/faustedition/ , generated graphs at http://faustedition.net/macrogenesis )
References
Allen, James F. 1983. “Maintaining Knowledge About Temporal Intervals.” Communication of Acm, 832–43.
Baharev, Ali, Hermann Schichl, and Arnold Neumaier. 2015. “An Exact Method for the Minimum Feedback Arc Set Problem,” December, 34. http://www.mat.univie.ac.at/~neum/ms/minimum_feedback_arc_set.pdf.
Bohnenkamp, Anne. 1994. "... das Hauptgeschäft nicht außer Augen lassend": die Paralipomena zu Goethes "Faust". Frankfurt am Main: Insel Verl.
Brüning, Gerrit, and Oliver Hahn. 2017. “Goethes Helena-Dichtung in Ursprünglicher Gestalt. Zum Methodischen Verhältnis von Materialanalyse Und Textkritik.” Editio 31 (1): 145–72. https://doi.org/10.1515/editio-2017-0009.
Fischer-Lamberg, Renate. 1955. “Untersuchungen Zur Chronologie von Faust II 2 Und 3.” Diss. phil. (masch.), Berlin.
Goethe, Johann Wolfgang. 2019. Faust. Historisch-Kritische Edition. Edited by Anne Bohnenkamp, Silke Henke, and Fotis Jannidis. Version 1.2 RC. Frankfurt am Main ; Weimar ; Würzburg. http://faustedition.net/.
Hoenen, Armin, and Gerrit Brüning. 2019. “Zur Stemmatologie Neuerer Überlieferungen.” DARIAH-DE Working Papers 29. urn:nbn:de:gbv:7-dariah-2019-1-3.
Holmen, Jon, and Christian-Emil Ore. 2010. “Deducing Event Chronology in a Cultural Heritage Documentation System - CAA Online Proceedings.” http://proceedings.caaconference.org/paper/17_holmen_ore_caa2009/.
Kahn, A. B. 1962. “Topological Sorting of Large Networks.” Commun. ACM 5 (11): 558–62. https://doi.org/10.1145/368996.369025.
Karp, Richard M. 1972. “Reducibility Among Combinatorial Problems.” In Complexity of Computer Computations: Proceedings of a Symposium on the Complexity of Computer Computations, Held March 20–22, 1972, at the IBM Thomas J. Watson Research Center, Yorktown Heights, New York, and Sponsored by the Office of Naval Research, Mathematics Program, IBM World Trade Corporation, and the IBM Research Mathematical Sciences Department, edited by Raymond E. Miller, James W. Thatcher, and Jean D. Bohlinger, 85–103. The IBM Research Symposia Series. Boston, MA: Springer US. https://doi.org/10.1007/978-1-4684-2001-2_9.
Schockaert, Steven, and Martine De Cock. 2008. “Temporal Reasoning About Fuzzy Intervals.” Artificial Intelligence 172 (8): 1158–93. https://doi.org/10.1016/j.artint.2008.01.001.
Vitt, Thorsten, and Gerrit Brüning. 2019. “Determining and Visualizing Genesis: A Digital Edition of Goethe’s Faust.” In DH2019 Book of Abstracts. Utrecht. https://dev.clariah.nl/files/dh2019/boa/0924.html.
Wissenbach, Moritz, Dietmar Pravida, and Gregor Middell. 2012. “Reasoning About Genesis or the Mechanical Philologist.” In Digital Humanities 2012: Conference Abstracts. Hamburg. http://www.dh2012.uni-hamburg.de/conference/programme/abstracts/reasoning-about-genesis-or-the-mechanical-philologist.1.html.